SVD(сингулярное) разложение
8.3.5. SVD-(сингулярное) разложение
Наиболее эффективными (но и ресурсоемкими) средствами решения произвольных СЛАУ (с матрицей А размера NxM) по методу наименьших квадратов являются так называемые полные ортогональные разложения, имеющие, по определению, вид A=UKVT.
Здесь U и V — ортогональные матрицы размером NxN и MхM соответственно, а k— матрица размера NxM, имеющая следующую структуру:
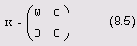
причем w — матрица размера kxk, где k — ранг исходной матрицы А.
Самое известное из ортогональных, SVD- (singular value decomposition) или сингулярное разложение — разложение вида A=USVT, где S — диагональная матрица, состоящая из нулей и расположенных на диагонали сингулярных чисел матрицы А. Расчет сингулярного разложения в Mathcad осуществляется при помощи пары встроенных функций:
- svds (A) — вектор, состоящий из сингулярных чисел;
- svd (A) — сингулярное разложение:
- А — действительная матрица.
Пример поиска сингулярного разложения сингулярной матрицы приведен в листинге 8.25, причем его последняя строка представляет собой проверку правильности найденного разложения. Подчеркнем, что вычисленные сингулярные числа находятся на главной диагонали средней матрицы разложения, а ее остальные элементы, по определению, равны нулю. Сравнивая матрицы из листинга 8.25, вы без труда разберетесь, каким образом следует выделять искомые матрицы сингулярного разложения из результата, поставляемого функцией svd.