Системы уравнений функция Find
5.2.1. Системы уравнений: функция Find
Рассмотрим решение системы N нелинейных уравнений с м неизвестными
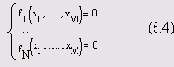
Здесь f1(x1, ..., хM), ..., fN (x1, ..., XM) — некоторые скалярные функции от скалярных переменных x1,x2, ..., хM и, возможно, от еще каких-либо переменных. Уравнений может быть как больше, так и меньше числа переменных. Заметим, что систему (5.4) можно формально переписать в виде
f(x)=0, (5.5)
где х — вектор, составленный из переменных x1,x2, ... ,хM, a f (х) — соответствующая векторная функция.
Вычислительный блок Given /Find
Для численного решения систем уравнений применяется тот же самый вычислительный блок, что и для символьных вычислений (см. разд. 5.1.1). Повторимся, что он состоит из ключевого слова Given, самой системы уравнений, записанной при помощи логических операторов панели Boolean (Булевы операторы), а также встроенной функции Find. Find(x1, ... ,хM) — встроенная функция для решения системы алгебраических уравнений и неравенств относительно переменных x1,...,xM. Значение функции Find представляет собой вектор, составленный из решений по каждой переменной.
Примечание 1
Примечание 1
Встроенная функция Find использует в качестве численного алгоритма один из градиентных методов (см. разд. 5.3). Этот факт налагает некоторые ограничения на уравнения системы, которые должны быть достаточно гладкими функциями своих аргументов.
Примечание 2
Примечание 2
При численных расчетах может быть найден только один из корней уравнения, в отличие от символьных вычислений, которые позволяют определить все имеющиеся корни.
Применение численного нахождения корней отличается от символьного двумя обстоятельствами:
- вместо оператора символьного вывода после функции Find следует использовать оператор численного вывода (знак равенства);
- перед вычислительным блоком Given/Find должны быть заданы начальные значения (guess value) для всех неизвестных, т. е. всем переменным x1, ... ,хM, относительно которых решается уравнение, следует предварительно присвоить некоторые численные значения, с которых и будет начинаться поиск корня. Таким образом, присвоение начального значения требует априорной информации о примерном местонахождении корня и связано с проблемой локализации корней, упомянутой в начале разд. 5.2.
Примечание 3
Примечание 3
Помните также о том, что, в отличие от символьного, для численного процессора необходимо задать числовые значения всех параметров, входящих в уравнение.
Одно уравнение с одним неизвестным
Рассмотрим в качестве примера (листинг 5.8) одно уравнение с одним неизвестным, которое уже решалось нами аналитически (см. листинги 5.1 и 5.2). Уравнение имеет три корня, как видно из графика, приведенного на Рисунок 5.4. Обратите внимание, что перед ключевым словом Given переменной х присваивается некоторое значение х=1. В остальном применение функции Find для решения уравнения не отличается от символьных расчетов.