График точности формулы (3 1)
Рисунок 3.5. График точности формулы (3.1) в зависимости от шага дельта (продолжение листинга 3.6)
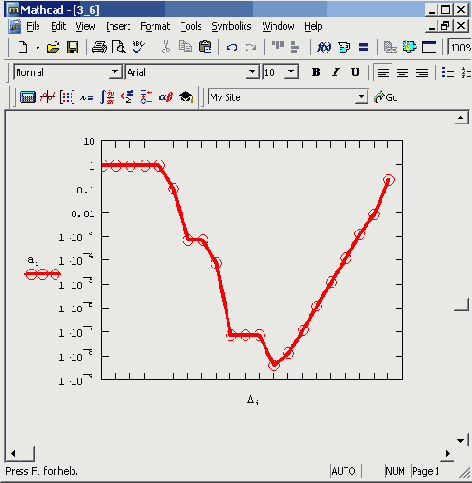
Если увеличение ошибки на правом конце графика является совершенно очевидным, поскольку, согласно формуле (3.1), чем больше А, тем больше погрешность, то рост ошибки при очень малых Д может, на первый взгляд, показаться неожиданным. Однако все дело в том, что, применяя разностную формулу, мы неявно полагали, что умеем точно вычислять значения функции f (х) в любой точке. Между тем, любые компьютерные вычисления сопряжены с неустранимыми погрешностями, в частности, обусловленными дискретным представлением чисел. Поэтому в реальности мы можем вычислить значение f (х) лишь с некоторой погрешностью 8, обусловленной (по крайней мере) заведомым округлением чисел при расчетах на компьютере.
В результате, при очень малом шаге разностные формулы означают вычитание друг из друга близких чисел. В этом случае ошибки вычисления функции f (х) становятся доминирующими и приводят к существенному росту суммарной погрешности вычисления разностной производной. Отсюда как раз и следует тот вывод, что значение шага следует выбирать "не очень малым", иначе ошибки вычисления f (х) неминуемо сделают результат дифференцирования неправильным. Глядя на Рисунок 3.5, легко сообразить, что в данном случае следует выбирать промежуточные значения Д, которые обеспечат минимальную (или почти минимальную) погрешность.
Следует подчеркнуть, что в зависимости от характера дифференцируемой функции диапазон приемлемых значений Л будет различным. Поэтому в каждом конкретном случае требуется совершать дополнительные шаги, тестирующие верность выбора шага для численного дифференцирования. Такая процедура, кстати говоря, заложена в адаптивном алгоритме дифференцирования, примененном в Mathcad, что делает его весьма надежным для численного расчета производной.
С учетом сказанного выше, с дифференцированием в Mathcad обычно не возникает сложных проблем. Исключение составляют функции, которые дифференцируются в окрестности сингулярной точки; например, для функции f (х)=1/х это будут точки вблизи х=0. При попытке найти ее производную при х=0 (Рисунок 3.6) будет выдано сообщение об одной из ошибок деления на ноль "Can't divide by zero" (Деление на ноль невозможно) или "Found a singularity while evaluating this expression. You may be dividing by zero" (Найдена сингулярность при вычислении этого выражения. Возможно, вы делите на ноль).