График разложений функции в ряд
Рисунок 3.13. График разложений функции в ряд в зависимости от порядка аппроксимации (продолжение листинга 3.21)
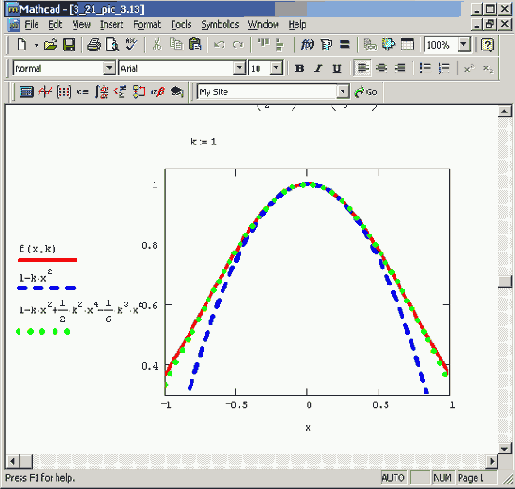
Видно, что разложение в ряд хорошо работает в окрестности точки х=0, а по мере удаления от нее все сильнее и сильнее отличается от функции. Естественно, что чем выше порядок аппроксимации, тем ближе к исходной функции располагается соответствующее разложение Тейлора.